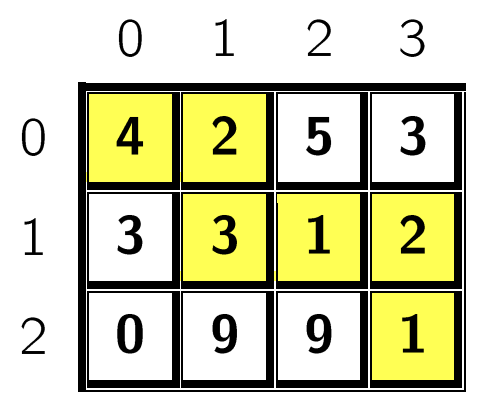
Lưới ô kích thước ~M \times N~, mỗi ô vuông điền một số tự nhiên không quá 6 chữ số. Chỉ hai ô chung cạnh mới có thể đi được trực tiếp sang nhau.

Ta gọi chi phí đường đi từ ô ~(x, y)~ tới ô ~(p, q)~ là tổng các số trên các ô thuộc đường đi. Ví dụ như một đường đi từ ô ~(0, 0)~ tới ô ~(2, 3)~ gồm các ô được tô màu vàng và chi phí là 13. Tất nhiên có nhiều đường đi nhưng ta chỉ quan tâm đến chi phí nhỏ nhất, trong trường hợp này đúng là bằng 13.

Xuất phát từ một ô ~(p, q)~ bất kỳ, ta có thể tính toán chi phí nhỏ nhất đi đến mọi ô khác trên lưới bằng nhiều cách, nhưng cuối cùng ta sẽ được một ma trận mà ô ~(x, y)~ điền chi phí thấp nhất từ ~(p, q)~ đến ~(x, y)~, ta gọi đây là ma trận chi phí.

Yêu cầu: cho lưới ~M \times N~, hãy tính số ~K~ là tổng tất cả các phần tử của ma trận chi phí tương ứng (~M~ và ~N~ không quá ~1000~).

Input:

• Dòng đầu ghi 4 số ~m, n, p~ và ~q~.
• ~M~ dòng tiếp sau: mỗi dòng ghi đúng ~N~ số là ~N~ giá trị điền trên dòng tương ứng.

Output:

• Số ~K~

Dữ liệu ứng với hình vẽ trên và xuất phát từ ô ~(0, 0)~

Sample Input 1

3 4 0 0
4 2 5 3
3 3 1 2
0 9 9 1

Sample Output 1

128

Giải thích: OUTPUT ~128~ ứng với tổng các số trên ma trận chi phí dưới đây: