Đề luyện tập môn thuật toán ứng dụng
Tìm cách đi lợi ích nhất cho robot
Nộp bài
Time limit: 5.0 /
Memory limit: 977M
Point: 1
Một bản đồ trò chơi gồm có ~N~ điểm dừng:
- Các điểm được đánh số từ ~1~ đến ~N~
- Trên mỗi điểm dừng đặt một món phần thưởng có giá trị ~10000 > V_k > 0~ ứng với số thứ tự ~k~ của điểm dừng đó
- Giữa hai điểm dừng thứ ~p~ và thứ ~q~, nếu có đường đi giữa chúng thì việc di chuyển sẽ mất thời gian là ~T_{p,q} (10000 > T_{p,q} = T_{q, p} > 0)~.
Một robot xuất phát ở điểm dừng số ~1~ có nhiệm vụ di chuyển đến điểm dừng số ~N~, nếu robot đi qua điểm dừng nào đó, nó có thể nhận được món phần thưởng ở điểm dừng đó.
Nhiệm vụ: Nhập thông tin về bản đồ trò chơi, hãy tính xem robot di chuyển đến điểm dừng số ~N~ nhanh nhất có thể nhận được tổng giá trị trưởng tối đa là bao nhiêu?
Input
- Dòng 1: Số ~N (N <= 1000)~
- Dòng 2: Các giá trị ~V_1, V_2, ..., V_N~
- Dòng 3: Số ~M~ (số lượng đường đi trên bản đồ)
- ~M~ dòng tiếp theo: Mỗi dòng ghi 3 số ~p, q~ và ~u~ trong đó ~u~ là thời gian di chuyển từ điểm ~p~ đến ~q~
Output
- Duy nhất một con số là giá trị tối đa của robot di chuyển đến ~N~ nhanh nhất, ghi 0 nếu không có đường đi
Sample Input 1
8
1 2 3 4 7 7 5 8
11
1 2 1
1 3 1
1 4 1
2 5 1
2 6 1
3 6 1
3 7 1
4 7 1
5 8 1
6 8 1
7 8 1
Sample Output 1
19
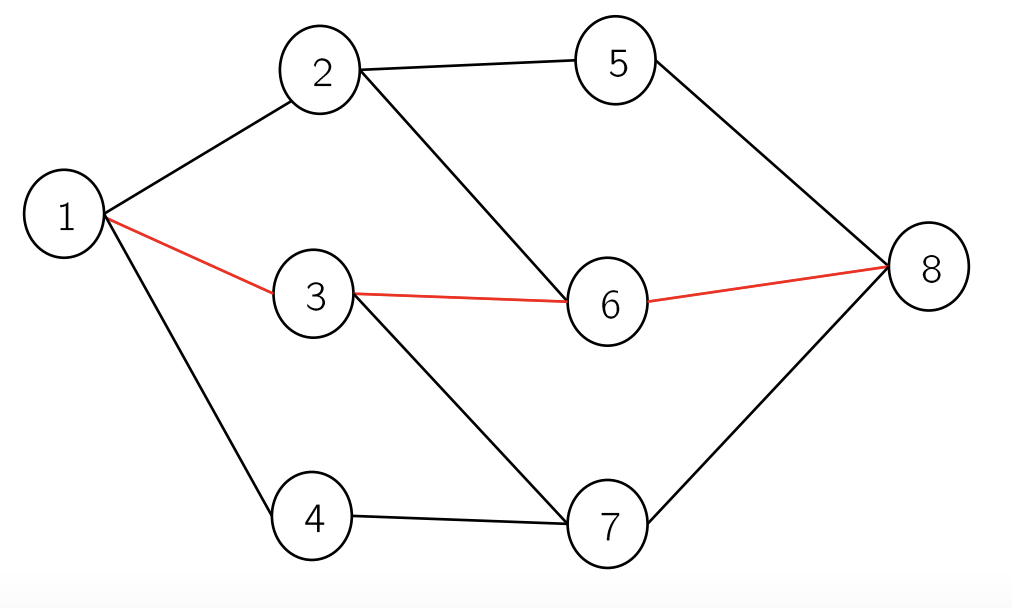
Hình vẽ dưới đây giải thích phương án đi của robot ứng với input mẫu phía trên (đường đỏ là đường tối ưu - độ dài 3 - tổng thưởng là 19):