Lớp Đội tuyển Olympic Tin học & ICPC 2023 - Buổi 06
Mã đi ngủ
Nộp bàiPoint: 100
Sau một ngày đi tuần vất vả trên cái bàn cờ vua kích thước ~n \times n~, cũng đã đến lúc quân Mã được nghỉ ngơi. Biết rằng hiện tại quân Mã đang đứng ở ô có tọa độ (m, n), hãy chỉ ra số bước nhảy ít nhất để di chuyển quân Mã đó về nhà ở ô (1, 1).
Đề bài có q truy vấn, mỗi truy vấn gồm tọa độ (m, n). Để được toàn bộ số điểm của 1 test bạn cần trả lời đúng q truy vấn này.
Input:
- Dòng đầu tiên chứa 2 số nguyên ~n, q~ ~(1 <= n <= 1000)~
- ~q~ dòng tiếp theo mỗi dòng chứa 2 số nguyên ~x_i, y_i~
Output:
- In ra ~q~ dòng, dòng thứ ~i~ là số bước nhảy ít nhất để di chuyển từ ô ~(x_i, y_i)~ về ô ~(1, 1)~. Trong trường hợp không đi được thì in ra
-1
Sample Input 1
3 4
1 3
1 1
2 1
2 2
Sample Output 1
2
0
3
-1
Sample Input 2
4 4
4 4
4 1
3 3
1 1
Sample Output 2
2
5
4
0
Tìm cách đi lợi ích nhất cho robot
Nộp bàiPoint: 100
Một bản đồ trò chơi gồm có ~N~ điểm dừng:
- Các điểm được đánh số từ ~1~ đến ~N~
- Trên mỗi điểm dừng đặt một món phần thưởng có giá trị ~10000 > V_k > 0~ ứng với số thứ tự ~k~ của điểm dừng đó
- Giữa hai điểm dừng thứ ~p~ và thứ ~q~, nếu có đường đi giữa chúng thì việc di chuyển sẽ mất thời gian là ~T_{p,q} (10000 > T_{p,q} = T_{q, p} > 0)~.
Một robot xuất phát ở điểm dừng số ~1~ có nhiệm vụ di chuyển đến điểm dừng số ~N~, nếu robot đi qua điểm dừng nào đó, nó có thể nhận được món phần thưởng ở điểm dừng đó.
Nhiệm vụ: Nhập thông tin về bản đồ trò chơi, hãy tính xem robot di chuyển đến điểm dừng số ~N~ nhanh nhất có thể nhận được tổng giá trị trưởng tối đa là bao nhiêu?
Input
- Dòng 1: Số ~N (N <= 1000)~
- Dòng 2: Các giá trị ~V_1, V_2, ..., V_N~
- Dòng 3: Số ~M~ (số lượng đường đi trên bản đồ)
- ~M~ dòng tiếp theo: Mỗi dòng ghi 3 số ~p, q~ và ~u~ trong đó ~u~ là thời gian di chuyển từ điểm ~p~ đến ~q~
Output
- Duy nhất một con số là giá trị tối đa của robot di chuyển đến ~N~ nhanh nhất, ghi 0 nếu không có đường đi
Sample Input 1
8
1 2 3 4 7 7 5 8
11
1 2 1
1 3 1
1 4 1
2 5 1
2 6 1
3 6 1
3 7 1
4 7 1
5 8 1
6 8 1
7 8 1
Sample Output 1
19
Hình vẽ dưới đây giải thích phương án đi của robot ứng với input mẫu phía trên (đường đỏ là đường tối ưu - độ dài 3 - tổng thưởng là 19):
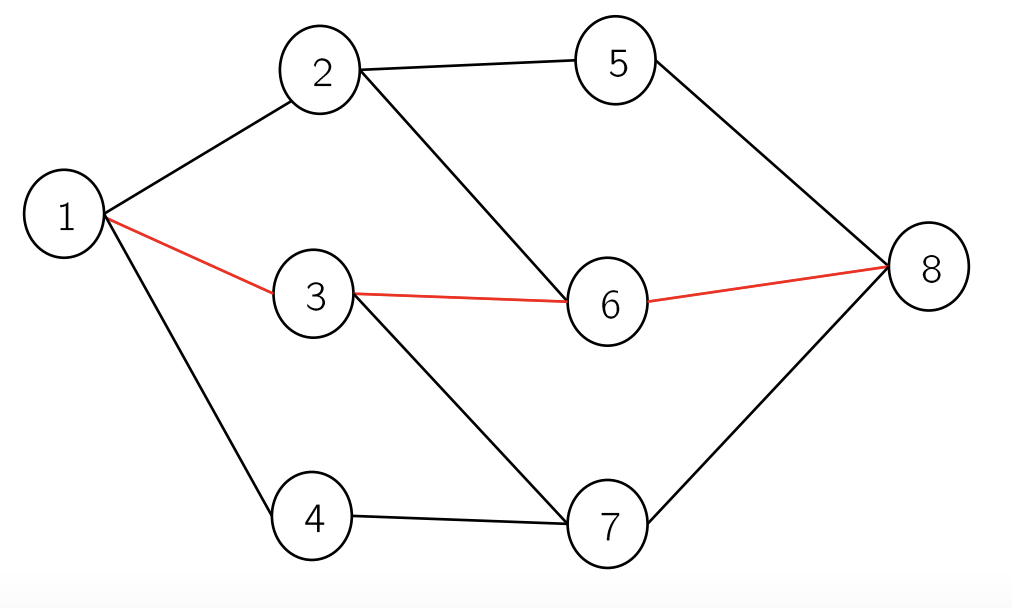
Đường đi có tích nhỏ nhất
Nộp bàiPoint: 100
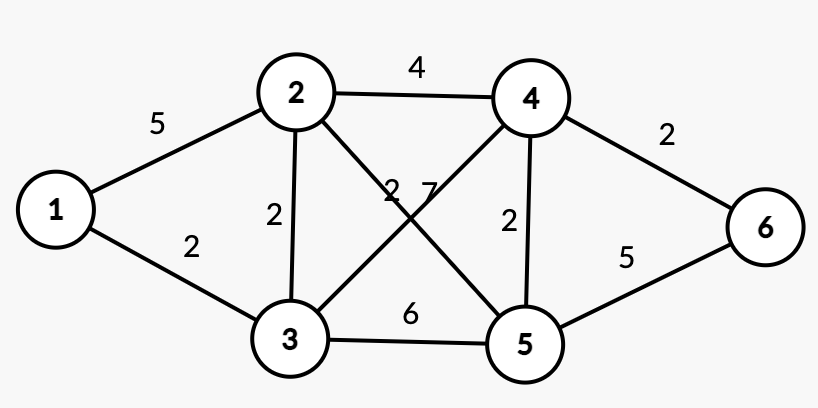
Cho đồ thị liên thông vô hướng G có ~n~ đỉnh (2 <= n <= 1000), ~m~ cạnh ~(n - 1 <= m <= \dfrac{n * (n - 1)}{2}~). Các đỉnh được đánh số từ 1, độ dài các cạnh không âm. Hãy chỉ ra đường đi từ đỉnh ~1~ đến đỉnh ~n~ có TÍCH độ dài các cạnh trên đường đi nhỏ nhất.
Input:
- Dòng đầu chứa 2 số nguyên ~n, m~
- ~m~ dòng tiếp theo chứa 3 số nguyên ~u, v, w~, thể hiện rằng cạnh nối đỉnh ~u~ và ~v~ có trọng số là ~w~ ~(0 <= w <= 10^5)~
Output:
- In ra các đỉnh trên đường đi có tích nhỏ nhất, nếu có nhiều đáp án thì in ra đáp án có thứ tự từ điển nhỏ nhất
- Nếu không có đáp án thì in ra
-1
Sample Input 1
6 10
1 2 5
1 3 2
2 3 2
2 4 4
2 5 7
3 4 2
3 5 6
4 5 2
4 6 2
5 6 5
Sample Output 1
1 3 4 6
Hình minh họa